Trigonometric Equations

SAT Questions that focus on Trigonometric Equations require knowledge of the following topics.

Let's find how to solve 8 typical trigonometric equations:

1) $sin(a)=sin(b)$

Consider the unit circle in the following figure:

Points A and A' are symmetrical in relation to axis $sin$, thus they have the same value for the $sin$ function. And the sum of arc A and arc A' equals to $\pi$, or 180º. If $sin(a)=sin(b)$:

$b=a+2n\pi$ (congruent angles), or
$a+b=\pi+2n\pi$ (symmetrical in relation to axis $sin$).

2) $cos(a)=cos(b)$

Consider the unit circle in the following figure:

Points A and A' (A'=-A) are symmetrical in relation to axis $cos$. Thus, if $cos(a)=cos(b)$:

$b=a+2n\pi$ (congruent angles), or
$b=-a+2n\pi$ (symmetrical in relation to axis $cos$).

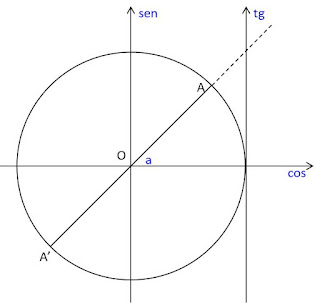
3) $tan(a)=tan(b)$

Consider the unit circle in the following figure:

Points A and A' are symmetrical in relation to the origin $O$, thus they have the same value for the $tan$ function. If $tan(a)=tan(b)$:

$b=a+n\pi$, where "n" is an integer.

4) $(a)sin(x)+(b)cos(x)=c$

Consider a right triangle's catheti "a" and "b". The hypotenuse of such a triangle will measure $\sqrt{a^2+b^2}$.
Therefore, the cosine of one of the angles of this triangle is given by the expression $cos(\alpha)=a/\sqrt{a^2+b^2}$; and the sine is given by $sin(\alpha)=b/\sqrt{a^2+b^2}$.

Now let's divide the trigonometric equation by $\sqrt{a^2+b^2}$:

$sin(x)*a/\sqrt{a^2+b^2}+cos(x)*b/\sqrt{a^2+b^2}=c/\sqrt{a^2+b^2}$

$sin(x)*cos(\alpha)+cos(x)*sen(\alpha)=c/\sqrt{a^2+b^2}$

$sin(x+\alpha)=c/\sqrt{a^2+b^2}$


Let's solve, for example: $sin(x)+\sqrt3*cos(x)=2$.

In this expression, $a=1$ and $b=\sqrt3$. Thus,

$\sqrt{a^2+b^2}=\sqrt{1^2+(\sqrt3)^2}=2$.

Dividing the trigonometric equation by "2":
$(1/2)sen(x)+(\sqrt3/2)cos(x)=2/2$
$cos(60)sen(x)+sen(60)cos(x)=1$
$sen(x+60)=1$
$x+60=90+2n\pi$

$x=30+2n\pi$

5) $(a)sin^2(x)+(b)sen(x)cos(x)+(c)cos^2(x)=d$

Dividing the two sides of the equation by $cos^2(x)$:

$(a)sin^2(x)/cos^2(x)+(b)sin(x)cos(x)/cos^2(x)+(c)cos^2(x)/cos^2(x)=d/cos^2(x)$
$(a)tan^2(x)+(b)sen(x)/cos(x)+c-(d)sec^2(x)=0$
$(a)tan^2(x)+(b)tan(x)+c-d.(1+tan^2(x))=0$

$(a-d).tan^2(x)+(b)tan(x)+(c-d)=0$ (a simple quadratic equation)

6) $(a)(sin(x)+cos(x))+(b)sin(x)cos(x)=d$

Consider $y=sin(x)+cos(x)$. Thus,

$y^2=sin^2(x)+2sin(x)cos(x)+cos^2(x)$
$y^2=[sin^2(x)+cos^2(x)]+2sin(x)cos(x)$
$y^2=1+2sin(x)cos(x)$
$sin(x)cos(x)=(y^2-1)/2$

Plugging this result into the trigonometric equation:
$(a)(sin(x)+cos(x))+(b)sin(x)cos(x)=d$
$(a)(y)+b(y^2-1)/2=d$
$ay+(b/2)y^2-b/2=d$

$(b/2).y^2+ay-b/2-d=0$ (again, a simple quadratic equation)

7) $sin^4(x)+cos^4(x)=a$

$[sin^2(x)+cos^2(x)]^2=sin^4(x)+2sin^2(x)cos^2(x)+cos^4(x)$
$(1)^2=sin^4(x)+2sin^2(x)cos^2(x)+cos^4(x)$
$sin^4(x)+cos^4(x)=1-2sin^2(x)cos^2(x)$
$sin^4(x)+cos^4(x)=1-2[sin(x).cos(x)]^2$
$sin^4(x)+cos^4(x)=1-2[0.5sin(2x)]^2$
$sin^4(x)+cos^4(x)=1-2*0,25sin^2(2x)$
$sin^4(x)+cos^4(x)=1-0.5sin^2(2x)$

Plugging this result into the trigonometric equation:
$sin^4(x)+cos^4(x)=a$
$1-0,5sin^2(2x)=a$

$sin^2(2x)=2(1-a)$

8) $sin^6(x)+cos^6(x)=a$

$sin^6(x)+cos^6(x)=(sin^2(x)+cos^2(x))(sin^4(x)-sin^2(x)cos^2(x)+cos^4(x))$

Therefore,
$(sin^2(x)+cos^2(x))(sin^4(x)-sin^2(x)cos^2(x)+cos^4(x))=a$
$(1)(sin^4(x)-sin^2(x)cos^2(x)+cos^4(x))=a$
$sin^4(x)+cos^4(x)-sin^2(x)cos^2(x)=a$
$[sin^2(x)+cos^2(x)]^2-2sin^2(x)cos^2(x)-sin^2(x)cos^2(x)=a$
$1-3sin^2(x)cos^2(x)=a$
$1-3sin^2(2x)/4=a$
$(3/4)sin^2(2x)=1-a$

$sin^2(2x)=(4-4a)/3$

Trigonometric Inequalities

The solution process for trigonometric inequalities follows the same steps as for solving trigonometric equations, as seen in the previous items. Once found the answers to the equation, we plug the results into the Unit Circle in order to find the solution to the inequality.

Solved SAT Practice Tests

Find Practice Tests in the following link: (not available yet)

SAT Practice Tests - Trigonometric Equations and

Additional Practice Tests - Trigonometric Equations